About Fahrenheit and Celsius
How temperature scales are related
If you look at the conversion formulas relating degrees Fahrenheit (°F) and Celsius (°C) that are implemented in our online converter, it does not immediately become obvious where the numerical factors are coming from. The following will give you a concise explanation.
To understand the relation between different temperature scales, one needs to look at the way each scale was originally set up. In the case of Celsius (also known as Centigrade), named after Anders Celsius (1701-1744), the scale is based on two well-defined reference points. One is the freezing point of pure water (at normal pressure), taken as zero, 0°C, of the scale. The other point, taken as 100°C, corresponds to the point when pure water boils (again, under normal pressure – in general, phase transformation temperatures depend on the pressure).
Fahrenheit scale, on the other hand, named after Gabriel Fahrenheit (1686-1736), was devised such that a temperature value lower than the water freezing point sets zero of the scale. To mark the lowest reference point of 0°F, the temperature of an equilibrated mixture of ice, water, and ammonium chloride was used. The second reference point, 32°F, corresponds to water freezing. An additional point, taken as 96°F, was chosen as the body temperature of a healthy human.
The following plot graphically illustrates the relation between °F and °C scales.
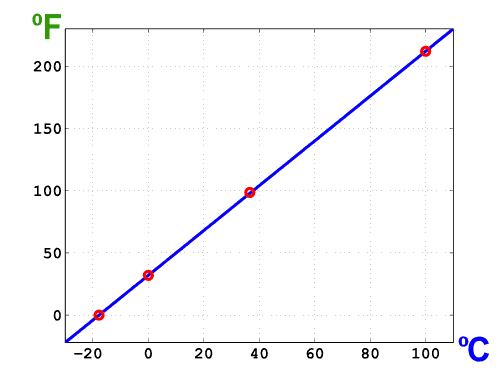
Reference points for both scales are indicated on the graph. The slope and intercept of this straight line are those specific numerical factors that appear in the Fahrenheit and Celsius conversion formulas.
It is important to mention that worldwide accepted SI (System International) system of units uses Kelvin as the reference unit for temperature. Kelvin (K) scale is based on a very unique reference point – the absolute zero of temperature. Temperature conversion between °C and K is very simple:
T [K] = T [C] + 273.15
Going from Kelvin to Fahrenheit is less straightforward. Our Kelvin converter page allows direct °F and K conversion and provides the corresponding equation.